アリコット数列(aliquot sequence)は、各項が直前の項の自分自身を除く約数の和となっている再帰数列です。自然数 kk から始まるアリコット数列は、約数関数 σ1σ1 によって次のように定義されます:
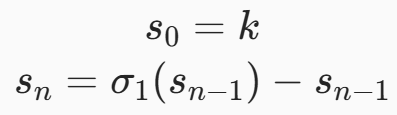
例えば、10から始まるアリコット数列は次のようになります:
- 10の約数の和(自分自身を除く):1 + 2 + 5 = 8
- 8の約数の和:1 + 2 + 4 = 7
- 7の約数の和:1
- 1の約数の和:0
したがって、10から始まるアリコット数列は 10, 8, 7, 1, 0 となります。
多くのアリコット数列は、素数、完全数、友愛数、社交数のいずれかで終了します。例えば、6のアリコット数列は 6, 6, 6, 6, ... という周期1の繰り返しになります。220のアリコット数列は 220, 284, 220, 284, ... という周期2の繰り返しになります。
アリコット数列は数学的に非常に興味深いテーマで、未解決の問題も多く存在します。例えば、カタランの予想では、すべてのアリコット数列は最終的に素数、完全数、友愛数、社交数のいずれかで終了するとされていますが、これが正しいかどうかはまだ証明されていません。
完全数、友愛数、社交数
完全数
完全数(Perfect Number)は、自分自身を除く約数の和がその数自身に等しい数です。例えば、最初の完全数は6です。6の約数は1, 2, 3, 6であり、1 + 2 + 3 = 6となります。次の完全数は28で、1 + 2 + 4 + 7 + 14 = 28です。完全数は非常に稀で、現在までに知られている完全数はすべて偶数です。
友愛数
友愛数(Amicable Numbers)は、2つの異なる自然数のペアであり、一方の数の自分自身を除く約数の和が他方の数に等しいものです。最も有名な友愛数のペアは220と284です。220の約数の和は1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284であり、284の約数の和は1 + 2 + 4 + 71 + 142 = 220です。
社交数
社交数(Sociable Numbers)は、友愛数の概念を拡張したもので、数の連鎖が閉じたループを形成するものです。例えば、社交数の一例として、4つの数の連鎖があり、各数の自分自身を除く約数の和が次の数に等しくなります。この連鎖が最終的に最初の数に戻ると、社交数と呼ばれます。

