アムダールの法則

マルチプロセッサによる並列化処理で得られる高速化率は、アムダールの法則を用いて計算することができます。この法則は、並列化できる部分と並列化できない部分の割合を考慮して、全体の高速化率を求めるものです.

アムダールの法則の式

アムダールの法則は次の式で表されます：

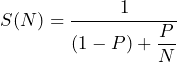
• S(N): N個のプロセッサを使用した場合の高速化率
• P: 並列化可能な部分の割合（0 ≦ P ≦ 1）
• N: 使用するプロセッサの数

計算例

例えば、プログラムの80%が並列化可能で、20%が並列化できない場合（P = 0.8）、プロセッサ数が4（N = 4）のときの高速化率は次のように計算されます：

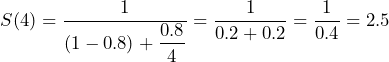
この場合、4つのプロセッサを使用すると、単一プロセッサに比べて2.5倍の高速化が得られることになります.

注意点

• 並列化の限界: 並列化できない部分があるため、プロセッサ数を増やしても無限に高速化できるわけではありません.
• オーバーヘッド: 実際のシステムでは、並列化に伴うオーバーヘッドも考慮する必要があります.

アムダールの法則は、並列化の効果を評価するための基本的な指標として広く利用されています。